Dátové štruktúry, ktoré by si ako informatik mal poznať - Stack a Queue

V tomto článku si vysvetlíme základné dátové štruktúry s ktorými sa vo svojej programátorskej kariére stretneš ešte veľa krát a sú dokonca aj základom mnohých komplexnejších algoritmov. Článok je štruktúrovaný do viacerých častí, kde si najprv povieme niečo bližšie o spomenutých dátových štruktúrach a neskôr prejdeme k ich samotnej implementácií v programovacom jazyku Python.

Stack

Názov tejto dátovej štruktúry by sme mohli do slovenčiny preložiť ako Zásobník a od tohto slova sa na úvod aj odrazíme. Predstavme si, že máme zásobník, do ktorého sa na šírku vôjde iba jedno ľubovoľné ovocie. Ak by sme do takéhoto zásobníka naukladali 5 typov ovocia, tak ako prvé vieme vybrať iba to, ktoré sme vložili ako posledné, a posledné vyberieme to, ktoré sme vložili ako prvé. Na rovnakom princípe funguje aj dátová štruktúra Stack, ktorej vizualizáciu z uvedeného príkladu môžeme vidieť na nasledujúcom obrázku:

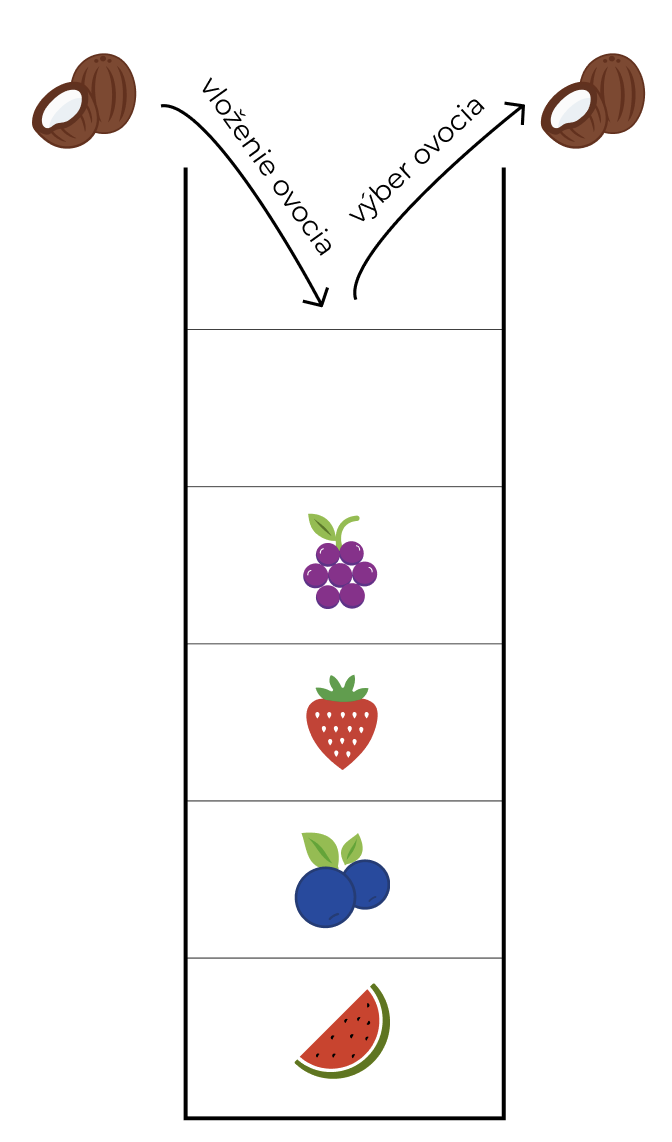
Princíp, ktorý sme si popísali na príklade zásobníka s ovocím sa odborne nazýva LIFO (po anglicky Last in First Out, čo do slovenčiny preložíme ako posledný dnu - prvý von). Ďalej si pod zásobníkom na ovocie predstavme pamäť počítača a pod ovocím rôzne typy dát. Tieto dáta môžu byť základné dátové typy ako čísla, znaky a podobne, ale aj vlastné triedy, ktoré sme si vytvorili buď my, alebo ktoré sú súčasťou programovacieho jazyka alebo knižnice, ktorú používame.

Kde má ale tak zdanlivo jednoduchá vec aj reálne využitie v informatike ? Príkladov si uvedieme hneď niekoľko. Stack sa používa na vyhodnocovanie zložitých aritmetických výrazov (pod zložité si môžeme predstaviť výraz s rôznym počtom zátvoriek, ktoré sú rôznych typov a používajú aj aritmetické operácie s rôznymi prioritami, tak ako tomu je v matematike, násobenie má vyššiu prioritu ako sčítanie a podobne). Iné využitie stacku môžeme nájsť aj v princípe, ktorý nazývame prehľadávanie do hĺbky alebo na ukladanie lokálnych premenných počas behu tvojho programu atď...

Keďže už máme predstavu čo je stack a aké má reálne využitie, mali by sme využiť, tak "silný nástroj" aký máme v rukách a voláme ho Python, v ktorom si ukážeme ako Stack implementovať a aké metódy by mal obsahovať.

Implementácia Stacku

Stack budeme implementovať pomocou spájaného zoznamu. Pred samotnou implementáciou si popíšeme metódy, ktoré by sme mali implementovať, ako aj ich význam:

push() - metóda, ktorú budeme používať na pridávanie prvkov do Stacku
pop() - metóda, ktorú budeme používať na vyberanie naposledy vloženého prvku zo Stacku (táto operácia zároveň aj daný prvok odstráni)
peek() - metóda, ktorú budeme používať na zistenie naposledy vloženého prvku do stacku (ale nevyberieme ho)
empty() - metóda, ktorú budeme používať na zistenie či je Stack prázdny

zavedieme si ešte výnimku, ktorú nazveme EmptyStackException a budeme ju "vyvolávať" v prípade, že je Stack už prázdny (túto výnimku by sme pri použití v aplikáciach vedeli odchytiť a vykonať potrebný kód podľa logiky aplikácie, išlo by napríklad do vypisanie hlášky pre používateľa aplikácie).

Finálny kód s ukážkou využitia popísaných metód:

INFORMATIKA_KU_KAVE = 'informatika_ku_kave'


class EmptyStackException(Exception):
    pass


class Node:
    def __init__(self, data):
        self.data = data
        # smerník na nasledujúci prvok v spájanom zozname
        self.next = None


class Stack:
    def __init__(self):
        self.__last = None

    def push(self, item):
        if self.__last is None:
            self.__last = Node(item)
        else:
            added_item = Node(item)
            added_item.next = self.__last
            self.__last = added_item

    def pop(self):
        if self.empty():
            raise EmptyStackException
        else:
            element_to_remove = self.__last
            self.__last = self.__last.next
            element_to_remove.next = None

        return element_to_remove.data

    def peek(self):
        if self.empty():
            raise EmptyStackException

        return self.__last.data

    def empty(self):
        return self.__last is None


if __name__ == "__main__":
    stack = Stack()

    for i in INFORMATIKA_KU_KAVE:
        stack.push(i)

    # vypíše evak_uk_akitamrofni
    while not stack.empty():
        print(stack.pop(), end="")

Aké sú časové zložitosti jednotlivých metód v našej implementácii ?

Ak ti hovorí niečo pojem časová zložitosť, tak táto časť článku je určená pre teba. Jednotlivé metódy našej implementácie majú nasledujúce časové zložitosti:

push() - má časovú zložitosť O(1), vyrobíme iba nový vrchol a meníme smerník
pop() - má časovú zložitosť O(1), zoberieme posledne vložený element zo spájaného zoznamu (jemu nastavíme smerník next na None) a premennú last nahradíme nasledujúcim prvkom v spájanom zozname
peek() - má časovú zložitosť O(1), pristupujeme iba k atribútu premennej last
empty() - má časovú zložitosť O(1), porovnávame či sa premenná last rovná None (prázdny spájaný zoznam)

Potrebujem si Stack programovať sám ?

Niektoré programovacie jazyky majú už túto dátovú štruktúru implementovanú za teba, ako príklad si uvedieme nasledujúce jazyky:

Java - import java.util.Stack;
C++ - #include <stack>;
C# - using System.Collections;

Queue

Názov tejto dátovej štruktúry by sme mohli do slovenčiny preložiť ako Front. Rovnako ako to bolo v prípade Stacku, ukážeme si príklad, ktorý určite poznáš z reálneho života. Je piatok večer, práve stojíš v obchode a chceš zaplatiť pri pokladni. Čo by to ale bol za piatok ak by pred tebou nestálo ešte veľa ľudí a ocitol si sa na konci radu ? A ako to v takom spravodlivom rade funguje ? Prvý platí ten, ktorý stál v rade ako prvý a ty, kedže si aktuálne posledný, sa dostaneš na rad ako posledný.... hmm, aké spravodlivé... Na rovnakom princípe funguje aj dátová štruktúra Queue, ktorej vizualizáciu z príkladu môžeme vidieť na nasledujúcom obrázku:

Princíp, ktorý sme si popísali na príklade ľudí v obchode sa odborne nazýva FIFO (po anglicky Fist In - First Out, čo do slovenčiny preložíme ako prvé dnu - prvé von). Rovnako ako pri Stacku si predstave namiesto ľudí rôzne typy dát, ktoré ukladáme v pamäti počítača.

Kde má Queue svoje reálne využitie v informatike ? Queue sa používa pri princípe, ktorý nazývame prehľadávanie do šírky, ďalej pri aplikáciách, ktoré posielajú emaily (tie sa dajú do queue a odosielajú sa v poradí v akom do queue boli vkladané) a v jej modifikáciách má svoje využitie pri hľadaní najkratšej cesty (Dijkstrov algoritmus, kde sa využíva prioritný front), alebo v operačných systémoch (čítanie vstupu z klávesnice, kde sa používa circular buffer) atď..

Keďže už máme predstavu čo je Queue a aké má reálne využitie, tak si predstavíme implementáciu tejto dátovej štruktúry v Pythone s metódami, ktoré by sme mali implementovať.

Implementácia Queue

Queue budeme implementovať pomocou spájaného zoznamu. Pred samotnou implementáciou si popíšeme metódy, ktoré by sme mali implementovať ako aj ich význam:

enqueue() - metóda, ktorú budeme používať pridávanie prvkov do Queue
dequeue() - metóda, ktorú budeme používať na vyberanie prvého vloženého prvku z Queue (táto operácia zároveň aj daný prvok odstráni)
front() - metóda, ktorú budeme používať na zistenie prvého prvku v queue (ale nevyberieme ho)
empty() - metóda, ktorú budeme používať na zistenie či je Queue prázdna

Zavedieme si ešte výnimku, ktorú nazveme EmptyQueueException a budeme ju "vyvolávať" v prípade, že je Queue už prázdná (túto výnimku by sme pri použití v aplikáciach vedeli odchytiť a vykonať potrebný kód podľa logiky aplikácie, išlo by napríklad do vypísanie hlášky pre používateľa aplikácie).

Finálny kód s ukážkou využitia popísaných metód:

INFORMATIKA_KU_KAVE = 'informatika_ku_kave'

class EmptyQueueException(Exception):
    pass

class Node:
    def __init__(self, data):
        self.data = data
        # smerník na nasledujúci prvok v spájanom zozname
        self.next = None


class Queue:
    def __init__(self):
        self.__start = None
        self.__end = None

    def enqueue(self, item):
        added_item = Node(item)

        if self.__end is None:
            self.__start = added_item
            self.__end = added_item
        else:
            self.__end.next = added_item
            self.__end = added_item

    def dequeue(self):
        if self.empty():
            raise EmptyQueueException

        element_to_remove = self.__start
        self.__start = element_to_remove.next

        if self.__start is None:
            self.__end = None

        return element_to_remove.data

    def front(self):
        if self.empty():
            raise EmptyQueueException

        return self.__start.data

    def empty(self):
        return self.__start is None


if __name__ == "__main__":
    queue = Queue()

    for i in INFORMATIKA_KU_KAVE:
        queue.enqueue(i)

    # vypíše informatika_ku_kave
    while not queue.empty():
        print(queue.dequeue(), end="")

Aké sú časové zložitosti jednotlivých metód v našej implementácii ?

Jednotlivé metódy našej implementácie majú nasledujúce časové zložitosti:

enqueue() - má časovú zložitosť O(1), vyrobíme iba nový vrchol a meníme smerníky
dequeue() - má časovú zložitosť O(1), prehadzujeme smerníky
front() - má časovú zložitosť O(1), pristupujeme k atribútu premennej start
empty() - má časovú zložitosť O(1), porovnávame či sa premenná start rovná None (prázdny spájaný zoznam)

Potrebujem si Queue programovať sám ?

Tak ako v prípade Stacku aj Queue už niektoré programovacie jazky majú implementovanú za teba, ako príklad si uvedieme:

Java - import java.util.Queue;
C++ - #include <stack>;
C# - using System.Collections;

V tomto článku sme si vysvetlili všetky potrebné informácie, ktoré by si o jedných z najdôležitejších dátových štruktúrach Stack a Queue mal vedieť. Aké by mali byť tvoje ďalšie kroky ? Môžeš si skúsiť implementovať vlastný Stack a Queue podľa ukážok kódu vo svojom obľúbenom programovacom jazyku, alebo sa pozrieť či už takáto implementácia v tvojom jazyku neexistuje. Rovnako sa môžeš pozrieť ako by sa tieto dátové štruktúry implementovali pomocou Python zoznamu a či by sa zmenili časové zložitosti operácií.

Ak sa ti tento článok páčil, tak si nezabudni prečítať aj ďalšie články na tomto webe a rovnako nás poteší ak tento článok prezdielaš ďalej ľuďom, ktorých zaujíma informatika.

Informatika ku káve - Richard